P1678 烦恼的高考志愿
题目背景
计算机竞赛小组的神牛 V 神终于结束了高考,然而作为班长的他还不能闲下来,班主任老 t 给了他一个艰巨的任务:帮同学找出最合理的大学填报方案。可是 v 神太忙了,身后还有一群小姑娘等着和他约会,于是他想到了同为计算机竞赛小组的你,请你帮他完成这个艰巨的任务。
题目描述
现有 m 所学校,每所学校预计分数线是 ai。有 n 位学生,估分分别为bi。
根据 n 位学生的估分情况,分别给每位学生推荐一所学校,要求学校的预计分数线和学生的估分相差最小(可高可低,毕竟是估分嘛),这个最小值为不满意度。求所有学生不满意度和的最小值。
输入格式
第一行读入两个整数 m,n。m 表示学校数,n 表示学生数。
第二行共有 m 个数,表示 m 个学校的预计录取分数。第三行有 n 个数,表示 n 个学生的估分成绩。
输出格式
输出一行,为最小的不满度之和。
先将分数线排序,然后用二分每次查找预录取分数,如果估分比查找下标出的录取分数低,则后面的分数线都比估分高,则令右指针指向此时的查找下标,反之则令左指针指向;
不满意度则令查找完后下标l或l-1指向的元素减去估分,然后累加
#include<bits/stdc++.h> using namespace std; long long a[1000005],s[1000000]; long long m,n; int main() { cin>>m>>n; for(long long i=1;i<=m;i++) { cin>>a[i];//预计分数线 } for(long long i=1;i<=n;i++) { cin>>s[i];//同学分数 } sort(a+1,a+m+1); long long sum=0; for(int i=1;i<=n;i++) { int l=0,r=m+1; while(l<r) { long long mid=(l+r)/2; if(a[mid]<=s[i]) { l=mid+1; } else { r=mid; } } if(a[1]>=s[i]) { sum+=a[1]-s[i]; } else { sum+=min(abs(a[l]-s[i]),abs(a[l-1]-s[i])); } } cout<<sum; return 0; }P2241 统计方形(数据加强版)
题目背景
1997年普及组第一题
题目描述
有一个 n×m 方格的棋盘,求其方格包含多少正方形、长方形(不包含正方形)。
输入格式
一行,两个正整数n,m(n≤5000,m≤5000)。
输出格式
一行,两个正整数,分别表示方格包含多少正方形、长方形(不包含正方形)。
#include<bits/stdc++.h> using namespace std; int main() { long long n,m,zfx=0,cfx=0; cin>>n>>m; for(int i=0;i<=n;i++) { for(int j=0;j<=m;j++) { if(i==j) { zfx+=(n-i)*(m-j); } else { cfx+=(n-i)*(m-j); } } } cout<<zfx<<" "<<cfx; }P1328 [NOIP2014 提高组]
题目背景
NOIP2014 提高组 D1T1
题目描述
石头剪刀布是常见的猜拳游戏:石头胜剪刀,剪刀胜布,布胜石头。如果两个人出拳一样,则不分胜负。在《生活大爆炸》第二季第 8 集中出现了一种石头剪刀布的升级版游戏。
升级版游戏在传统的石头剪刀布游戏的基础上,增加了两个新手势:
斯波克:《星际迷航》主角之一。
蜥蜴人:《星际迷航》中的反面角色。
这五种手势的胜负关系如表一所示,表中列出的是甲对乙的游戏结果。
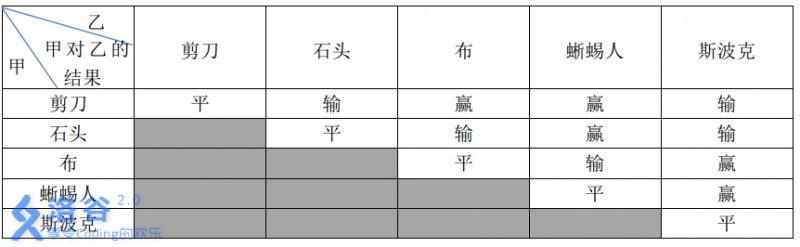
现在,小 A 和小 B 尝试玩这种升级版的猜拳游戏。已知他们的出拳都是有周期性规律的,但周期长度不一定相等。例如:如果小 A 以 石头-布-石头-剪刀-蜥蜴人-斯波克 长度为 66 的周期出拳,那么他的出拳序列就是 石头-布-石头-剪刀-蜥蜴人-斯波克-石头-布-石头-剪刀-蜥蜴人-斯波克-...,而如果小 B 以 剪刀-石头-布-斯波克-蜥蜴人 长度为 55 的周期出拳,那么他出拳的序列就是 剪刀-石头-布-斯波克-蜥蜴人-剪刀-石头-布-斯波克-蜥蜴人-...。
已知小 A 和小 B 一共进行 N 次猜拳。每一次赢的人得 11 分,输的得 00 分;平局两人都得 00 分。现请你统计 N 次猜拳结束之后两人的得分。
输入格式
第一行包含三个整数:N,NA,NB,分别表示共进行 N 次猜拳、小 A 出拳的周期长度,小 B 出拳的周期长度。数与数之间以一个空格分隔。
第二行包含 NA 个整数,表示小 A 出拳的规律,第三行包含NB 个整数,表示小 B 出拳的规律。其中,0 表示 剪刀,1 表示 石头,2 表示 布,3 表示 蜥蜴人,4 表示 斯波克。数与数之间以一个空格分隔。
输出格式
输出一行,包含两个整数,以一个空格分隔,分别表示小 A、小 B 的得分。
打表暴力秒了
#include<bits/stdc++.h> using namespace std; int a[205],b[205]; int N,Na,Nb; int main() { cin>>N>>Na>>Nb; for(int i=1;i<=Na;i++) { cin>>a[i]; } for(int i=1;i<=Nb;i++) { cin>>b[i]; } int sa=0; int sb=0; int ca=0; int cb=0; for(int k=1;k<=N;k++) { sa++; sb++; if(sa>Na)sa=1; if(sb>Nb)sb=1; if(a[sa]==0&&b[sb]==1)cb++; if(a[sa]==0&&b[sb]==2)ca++; if(a[sa]==0&&b[sb]==3)ca++; if(a[sa]==0&&b[sb]==4)cb++; if(a[sa]==1&&b[sb]==0)ca++; if(a[sa]==1&&b[sb]==2)cb++; if(a[sa]==1&&b[sb]==3)ca++; if(a[sa]==1&&b[sb]==4)cb++; if(a[sa]==2&&b[sb]==0)cb++; if(a[sa]==2&&b[sb]==1)ca++; if(a[sa]==2&&b[sb]==3)cb++; if(a[sa]==2&&b[sb]==4)ca++; if(a[sa]==3&&b[sb]==0)cb++; if(a[sa]==3&&b[sb]==1)cb++; if(a[sa]==3&&b[sb]==2)ca++; if(a[sa]==3&&b[sb]==4)ca++; if(a[sa]==4&&b[sb]==0)ca++; if(a[sa]==4&&b[sb]==1)ca++; if(a[sa]==4&&b[sb]==2)cb++; if(a[sa]==4&&b[sb]==3)cb++; } cout<<ca<<" "<<cb; return 0; }P8647 [蓝桥杯 2017 省 AB] 分巧克力
题目描述
儿童节那天有 K 位小朋友到小明家做客。小明拿出了珍藏的巧克力招待小朋友们。
小明一共有 N 块巧克力,其中第 i 块是 Hi×Wi 的方格组成的长方形。
为了公平起见,小明需要从这 N 块巧克力中切出 K 块巧克力分给小朋友们。切出的巧克力需要满足:
-
形状是正方形,边长是整数。
-
大小相同。
例如一块 6×5 的巧克力可以切出 6 块2×2 的巧克力或者 2 块3×3 的巧克力。
当然小朋友们都希望得到的巧克力尽可能大,你能帮小 Hi 计算出最大的边长是多少么?
输入格式
第一行包含两个整数N 和 K。(1≤N,K≤105)。
以下 N 行每行包含两个整数 Hi 和Wi。(1≤Hi,Wi≤105)。
输入保证每位小朋友至少能获得一块1×1 的巧克力。
输出格式
输出切出的正方形巧克力最大可能的边长。
因为每块巧克力大小都要一样,而且是正方形的
所以我们可以用二分来查找每次的巧克力边长,每次的边长最长是原来巧克力的最大边长
然后分割之后累加看能否满足,不能满足则缩小
#include<bits/stdc++.h> using namespace std; int n,k; int a[100005],b[100005]; bool judge(int mid) { long long ans=0; for(int i=1;i<=n;i++) { ans+=(a[i]/mid)*(b[i]/mid); } if(ans>=k) return true; else return false; } int main() { cin>>n>>k; int maxs=0; for(int i=1;i<=n;i++) { cin>>a[i]>>b[i]; maxs=max(a[i],max(maxs,b[i])); } int l=0,r=2*maxs; while(l<r) { int mid=(l+r)/2; if(judge(mid)) { l=mid+1; } else { r=mid; } } cout<<l-1; }P8707 [蓝桥杯 2020 省 AB1] 走方格
题目描述
在平面上有一些二维的点阵。
这些点的编号就像二维数组的编号一样,从上到下依次为第 11 至第 n 行,从左到右依次为第 11 至第 m 列,每一个点可以用行号和列号来表示。
现在有个人站在第 11 行第 11 列,要走到第 n 行第 m 列。只能向右或者向下走。
注意,如果行号和列数都是偶数,不能走入这一格中。
问有多少种方案。
输入格式
输入一行包含两个整数 n,m。
输出格式
输出一个整数,表示答案。
动态规划
#include<bits/stdc++.h> using namespace std; int dp[35][35]={0}; int n,m,i,j; int main() { cin>>n>>m; for(i=1;i<=m;i++) { for(j=1;j<=n;j++) { if(i==1&&j==1) { dp[i][j]=1; continue; } if(i%2==0&&j%2==0) { dp[i][j]=0; continue; } dp[i][j]=dp[i-1][j]+dp[i][j-1]; } } cout<<dp[m][n]; }原文链接:https://blog.csdn.net/2301_81794044/article/details/136179283?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522171910939516800186513135%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fblog.%2522%257D&request_id=171910939516800186513135&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~blog~first_rank_ecpm_v1~times_rank-12-136179283-null-null.nonecase&utm_term=2024%E5%B9%B4%E9%AB%98%E8%80%83%E5%88%86%E6%95%B0%E7%BA%BF